

Then, slope of the line segment PP', m 2 = \(\frac 2\)) Let (x', y') be the co- ordinates of the point P'. Then P' is the image of the point P under reflection about the line y = x. Draw perpendicular PM from the point P to the line y = x and produce it to the point P' such that PM = MP'. Then, slope of the line, m 1 = tan 45° = 1. Y = x is the equation of the line which makes an angle of 45° with the positive direction of X- axis. Hence, if R denotes the reflection in the line x = k, then: ∴ Image of point P (x, y) after reflection in the line x = k is P' (2k - x, y). ∴ Co- ordinates of the point P' are (2k - x, y). Since, M is the mid- point of the line segment PP', then by mid- point formula, Then P' is the image of P after reflection in the line x = k. Draw a perpendicular PM from P to the line x = k and produce it to the point P' such that PM = MP'. So, the reflection in a line parallel to Y- axis means reflection in the line x = k. The equation of a line parallel to Y- axis is given by x = k where k is X - intercept of the line. Reflection in the line parallel to Y- axis.Hence, if R denotes the reflection in the line y = k, then:
∴ Image of point P (x, y) after reflection in the line y = k is P' (x, 2k - y). ∴ Co- ordinates of the point P' are (x, 2k - y). Since, M is the mid-point of the line segment PP', then by mid- point formula, Let thye co- ordinates of P' be (x', y'). Then P' is the image of P after reflection in Draw a perpendicular PM from P to the line y = k and produce it to the point P' such that PM = PM'. So, reflection in the line parallel to X- axis means reflection in the line y = k. The equation of a line parallel to X- axis is given by y = k where k is Y- intercept of the line.
Reflection in the line parallel to X- axis. Hence, if R y denotes the reflection in Y- axis, then: ∴ Image of point P(x, y) after reflection in Y- axis P' (-x, y). ∴ Co- ordinates of the point P' are (-x, y). Since M is the mid-point of line segment PP', then by mid- point formula, Then P' is the image of P after reflection in Y- axis. Draw a perpendicular PM from the point P to the Y- axis and produce it to the point P' such that PM = MP'. So, reflection in Y- axis means reflection in the line x = 0. Hence, if R x denotes the reflection in X- axis, then:Įquation of Y- axis is x = 0. ∴ Image of point P(x, y) after reflection in X- axis is P'(x, -y). Since L is the mid- point of line segment PP', then by mid- point formula, Then P' is the image of P after reflection in X- axis. Draw a perpendicular PL from the point P to the X- axis and produce it to the point P' such that PL = LP'. So, reflection in X- axis means reflection in the line y = 0. In reflection, the object figure and its image figure are congruent to each other.Įquation of X- axis is y = 0. The points on the axis of reflection are invariant points.į. XX'is perpendicular bisector of AA', BB' and CC' as in fig 3.ĭ. The lines joining the same ends of the object and image are perpendicular to reflecting axis.Īxis of reflection is the perpendicular bisector of the line segment joining same ends of object and image. It means top remains at the top, bottom remains at the bottom but left side goes to the right side and right side goes to the left side as shown in fig 2.Ĭ. The shape of objects and images are laterally inverted. Coordinates can be used for finding images of geometrical figures after the reflection in the lines like X- axis, Y- axis, a line parallel to X- axis, a line parallel to Y- axis, the line y = x, the line y = -x, etc.The distance of the object from the axis of reflection is equal to the distance of reflection is equal to the distance of the image from the axis is a reflection.ī. When geometrical figures are reflected in the axis of reflection, the following properties are found.Ī. Characteristics of reflection of geometrical figures in the axis. The mirror line is also called the axis of reflection. 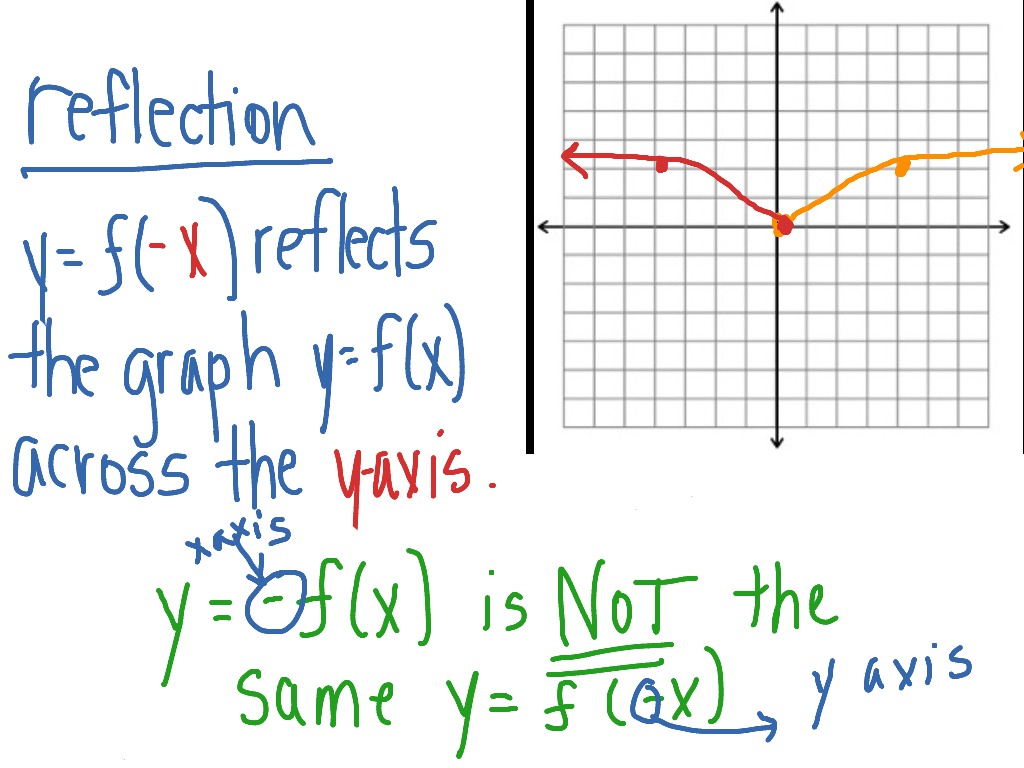
It means the mirror line is perpendicular bisector of the line segment joining object and image. The line work as a plane mirror. In reflection, the line joining the object and the image is perpendicular to the mirror line. A reflection is a transformation that flips a figure across a line.







 0 kommentar(er)
0 kommentar(er)
